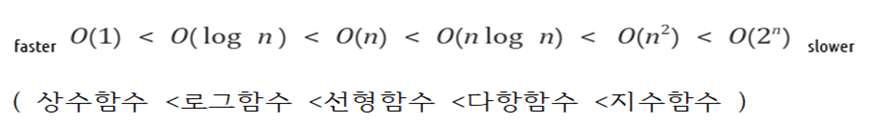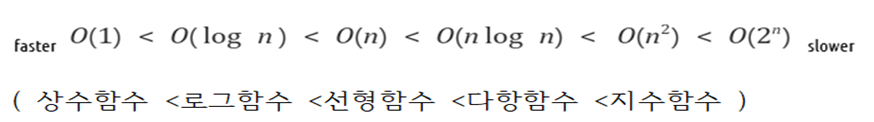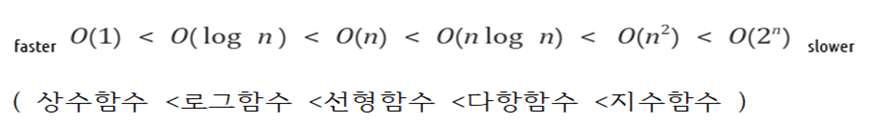알고리즘의 이해
알고리즘
- 문제해결 방법을 추상화하여 단계적 절차를 논리적으로 기술해 놓은 명세서
알고리즘의 조건
- 입력 input : 알고리즘 수행에 필요한 자료가 외부에서 입력으로 제공 될 수 있어야 한다.
- 출력 output : 알고리즘 수행 후 하나 이상의 결과를 출력해야 한다.
- 명확성 definiteness : 수행할 작업의 내용과 순서를 나타내는 알고리즘의 명령어들은 명확하게 명세 되어야 한다.
- 유한성 finiteness : 알고리즘은 수행 뒤에 반드시 종료되어야 한다.
- 효과성 effectiveness : 알고리즘의 모든 명령어들은 기본적이며 실행이 가능해야 한다.

알고리즘 = 자료를 이용하여 절차에 맞게 연산을 하는것
알고리즘의 표현 방법
알고리즘의 표현 방법의 종류
- 자연어를 이용한 서술적 표현 방법
- 순서도 Flow chart를 이용한 도식화 표현 방법
- 프로그래밍 언어를 이용한 구체화 방법
- 가상코드 Pseudo-code를 이용한 추상화 방법
순서도를 이용한 도식화
- 순서도의 예) 1부터 5까지의 합을 구하는 알고리즘

가상코드를 이용한 추상화
- 가상코드, 즉 알고리즘 기술언어 ADL, Algorithm Description Language를 사용하여 프로그래밍 언어의 일반적인 형태와 유사하게 알고리즘을 표현
- 특정 프로그래밍 언어가 아니므로 직접 실행은 불가능
- 일반적인 프로그래밍 언어의 형태이므로 원하는 특정 프로그래밍 언어로의 변환 용이
가상코드의 형식
기본 요소
기호
− 변수, 자료형 이름, 프로그램 이름, 레코드 필드 명, 문장의 레이블 등을 나타냄
− 문자나 숫자의 조합. 첫 문자는 반드시 영문자 사용.
자료형
−정수형과 실수형의 수치 자료형, 문자형, 논리형, 포인터, 문자열 등의 모든 자료형 사용
연산자
−산술연산자, 관계연산자, 논리연산자
지정문 형식과 예

조건문
- 조건에 따라 실행할 명령문이 결정되는 선택적 제어구조를 만든다.
- if 문의 형식과 제어흐름

다단계 조건문
- 중첩 if 문의 형식과 제어 흐름
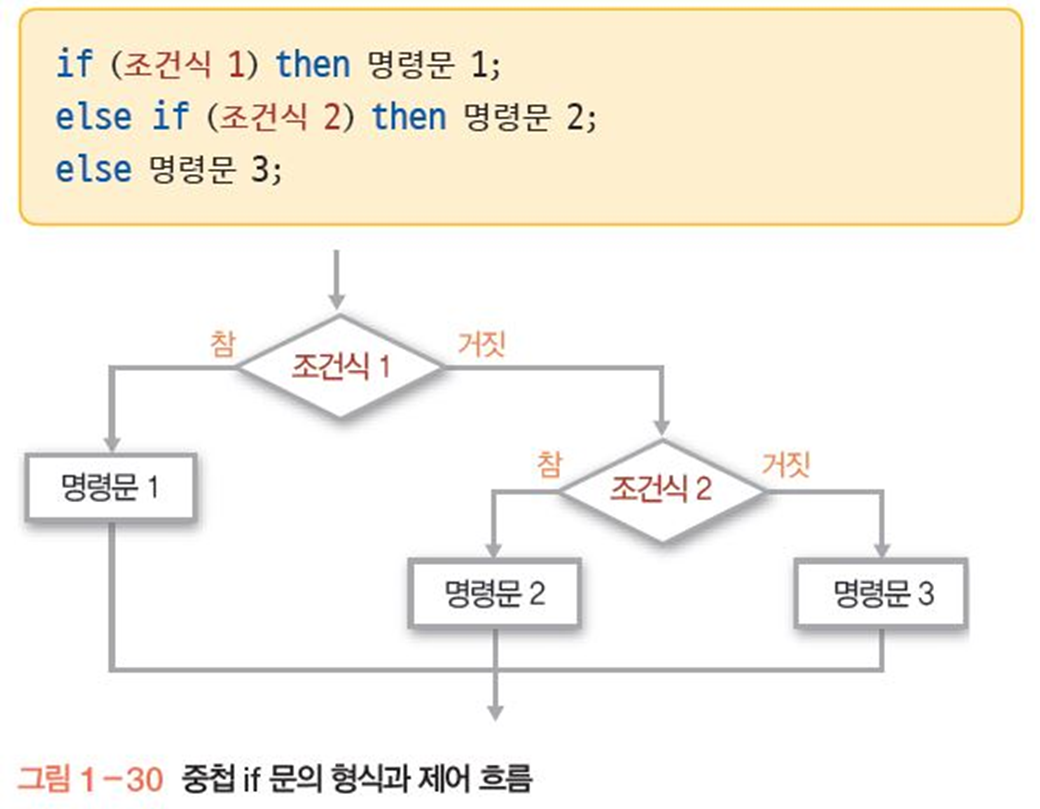
중첩 if문 사용 예) 평균 점수에 따른 등급 계산하기

case 문
- 여러 조건식 중에서 해당 조건을 찾아서 그에 대한 명령문을 수행
- 중첩 if 문으로 표현 가능
- 형식과 제어흐름
case 문 예) 평균 점수에 따른 등급 계산하기
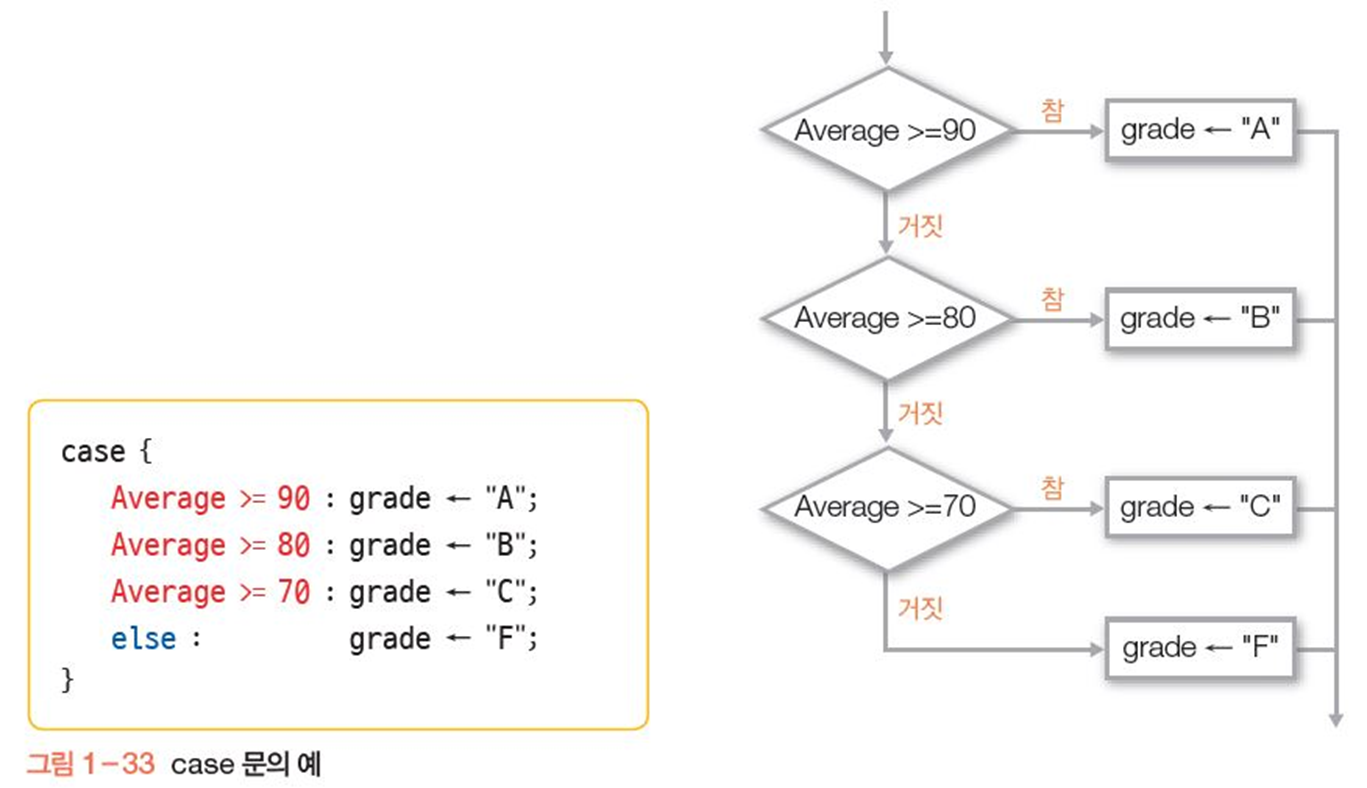
반복문
일정한 명령을 반복 수행하는 루프(loop) 형태의 제어구조
for 문 - 형식과 제어흐름
while – do 문 - 형식과 제어흐름

do-while 문 - 형식과 제어흐름

함수문
- 처리작업 별로 모듈화하여 만든 부프로그램
형식과 예

알고리즘의 성능분석
알고리즘 성능 분석 기준
- 기준에는 정확성, 명확성, 수행량, 메모리 사용량, 최적성 등 있음
정확성 : 올바른 자료 입력 시 유한한 시간 내에 올바른 결과 출력 여부
명확성 : 알고리즘이 얼마나 이해하기 쉽고 명확하게 작성되었는가
수행량 : 일반적인 연산 제외, 알고리즘 특성 나타내는 중요 연산 모두 분석
메모리 사용량
최적성 : 가장 중요
알고리즘 성능 분석 방법
공간 복잡도
알고리즘을 프로그램으로 실행하여 완료하기까지 필요한 총 저장 공간의 양
공간 복잡도 = 고정 공간 + 가변 공간
시간 복잡도
알고리즘을 프로그램으로 실행하여 완료하기까지의 총 소요시간
시간 복잡도 = 컴파일 시간 + 실행 시간
− 컴파일 시간 : 프로그램마다 거의 고정적인 시간 소요
− 실행 시간 : 컴퓨터의 성능에 따라 달라질 수 있으므로 실제 실행시간 보다는 명령문의 실행 빈도수에 따라 계산
실행 빈도수의 계산
−지정문, 조건문, 반복문 내의 제어문과 반환문은 실행시간 차이가 거의 없으므로 하나의 단위시간을 갖는 기본 명령문으로 취급
시간 복잡도 예) 피보나치 수열 알고리즘의 빈도수 구하기

시간 복잡도 n<0, n=0, n=1의 경우에 대한 실행 빈도수

알고리즘 성능 분석 표기법
■ 빅오 표기법 (big-O notation) 이란?
- 빅오 표기법은 알고리즘의 효율성을 표기해주는 표기법이다.
- 알고리즘의 효율성은 데이터 개수(n)가 주어졌을 때 덧셈, 뺄셈, 곱셈 같은 기본 연산의 횟수를 의미한다.
- 빅오 표기법은 보통 알고리즘의 시간 복잡도와 공간 복잡도를 나타내는데 주로 사용함.
- 시간 복잡도는 알고리즘의 시간 효율성을 의미하고, 공간 복잡도는 알고리즘의 공간 (메모리) 효율성을 의미한다.
- 시간과 공간 복잡도를 나타내는 방법으로는 점근 표기법이라고 해서
① 빅오(Big-O) ② 빅오메가(big-Ω) ③ 빅세타(big-Θ) 표기법이 있다.
■ 빅오 표기법(Big-O)은 알고리즘 효율성을 상한선 기준으로 표기한다.
- 알고리즘 효율성은 값이 클수록 즉, 그래프가 위로 향할수록 비효율적임을 의미한다.
■ 빅오메가(big-Ω)는 하한선을 기준으로하고, 빅세타(big-Θ)는 상한선과 하한선의 사이를 기준으로 표기한다.
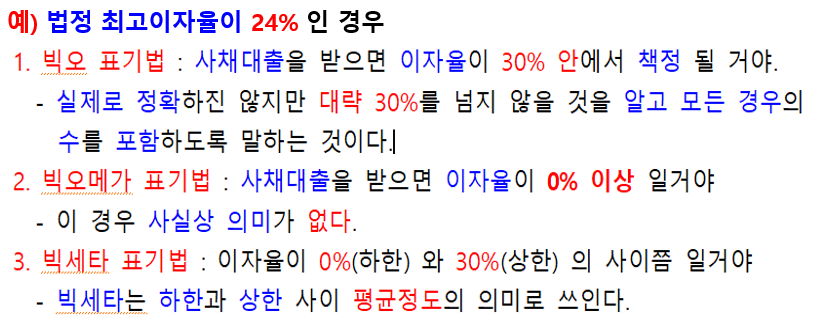
빅-오 표기법 (Big-O)
O(f(n))과 같이 표기, “Big Oh of f(n)”으로 읽음
수학적 정의
−함수 f(n)과 g(n)이 주어졌을 때, 모든 n≥n0에 대하여 |f(n)| ≤ c |g(n)|을 만족하는 상수 c와 n0이 존재하면, f(n) = O(g(n))이다.
함수의 상한을 나타내기 위한 표기법
−최악의 경우에도 g(n)의 수행 시간 안에는 알고리즘 수행 완료 보장
먼저 실행 빈도수를 구하여 실행 시간 함수를 찾고, 이 함수 값에 가장 큰 영향을 주는 n에 대한 항을 한 개 선택하여 계수는 생략하고 O의 오른쪽 괄호 안에 표시
[알고리즘 1-1]의 피보나치 수열에서 실행 시간 함수는 4n+2이고, 가장 영향이 큰 항은 4n인데 여기에서 계수 4를 생략하여 O(n)으로 표기

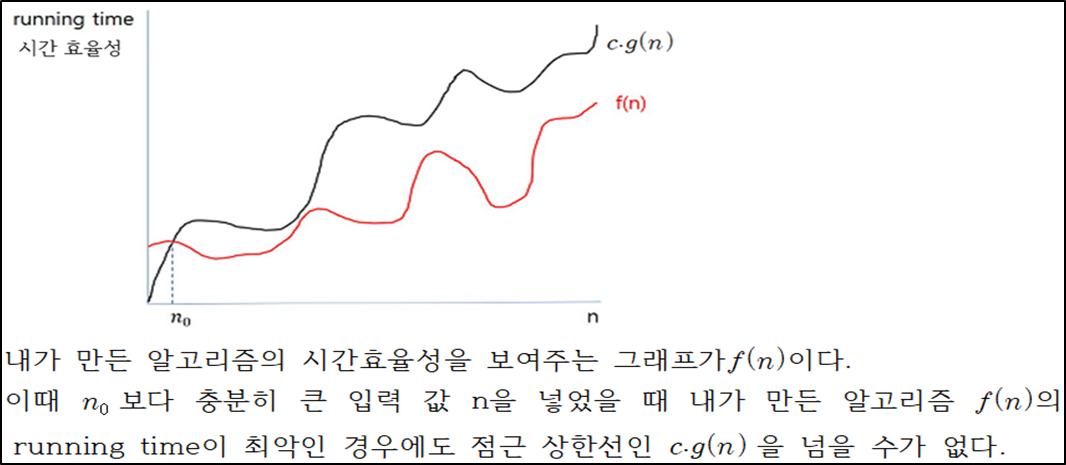
빅-오메가 표기법 (big-Ω)
Ω(f(n))과 같이 표기, “Big Omega of f(n)”으로 읽음
수학적 정의
−함수 f(n)과 g(n)이 주어졌을 때, 모든 n≥n0에 대하여 |f(n)| ≥ c |g(n)|을 만족하는 상수 c와 n0이 존재하면, f(n) = Ω(g(n))이다.
함수의 하한을 나타내기 위한 표기법
어떤 알고리즘의 시간 복잡도가 Ω(g(n))으로 분석되었다면, 이 알고리즘 수행에는 적어도 g(n)의 수행 시간이 필요함을 의미
빅-세타 표기법 (big-Θ)
θ(f(n))과 같이 표기, “Big Theta of f(n)”으로 읽음
수학적 정의
−f(n)과 g(n)이 주어졌을 때, 모든 n≥n0에 대하여 c1 |g(n)| ≤ f(n) ≤ c2 |g(n)을 만족하는 상수 c1, c2와 n0이 존재하면, f(n) = θ(g(n))이다
상한과 하한이 같은 정확한 차수를 표현하기 위한 표기법
- f(n)= θ (g(n))이 되려면 f(n)= O(g(n))이면서 f(n)= Ω(g(n))이어야 함
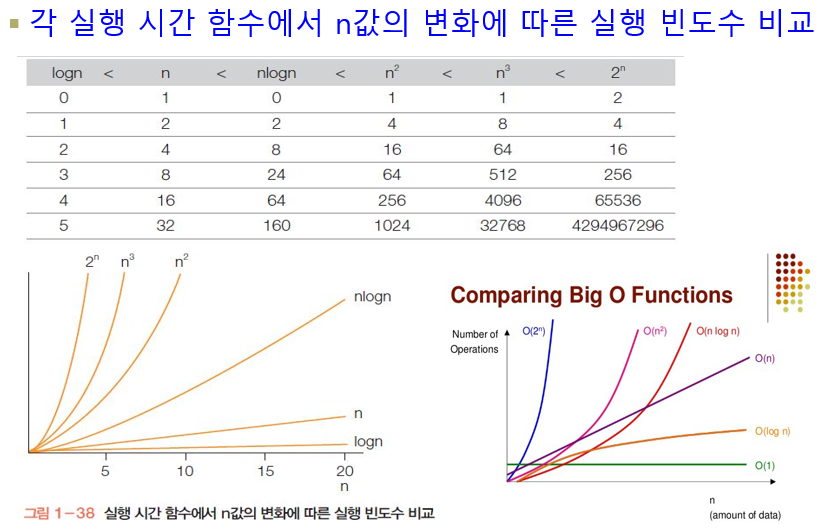
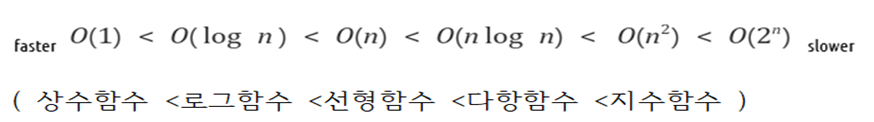

빅 오의 자료구조 적용 예